一个萝卜一个坑:计数排序
计数数组是计数器变量的“升级版本”,它通过巧妙运用数组下标来完成计数工作。
预习篇
1. 计数器变量的使用
给定100个小于100的正整数,
- 如何统计其中数字7出现的次数?
- 如何统计其中数字3、5、7出现的次数?
- 如何统计其中数字1到100出现的次数?
显然学过循环的我们知道,可以通过定义一个计数器变量来解决第一个问题:
int cnt = 0;for (int i = 0; i < 100; i++) { int t; scanf("%d", &t); if (t == 7) cnt++;}printf("%d", cnt);对于问题2,统计的数字个数变为了3个,你一定知道要怎么做~
xxxxxxxxxx// 这时候只要将计数器变量从1个变为3个就好啦~int cnt3 = 0, cnt5 = 0, cnt7 = 0;for (int i = 0; i < 100; i++) { int t; scanf("%d", &t); if (t == 3) cnt3++; if (t == 5) cnt5++; if (t == 7) cnt7++;}printf("%d %d %d", cnt3, cnt5, cnt7);巩固计数器的练习:
不过,当问题再次升级,需要统计数字1到100,每一个数字出现的次数时,按照上面的思路,难道要定义100个变量?这...😅😅😅,确实听起来就不是什么好主意。
回忆一下最开始学习数组,也是因为要保存的数据元素较多,和现在的情形类似。
课后篇

一、咚咚~计数数组横空出世
计数数组可以看为是对计数器变量的一个升级🆙,也是对数组下标的灵活运用。下面先来回答预习篇最后1个问题(当然相信你心里早已有了答案~)。



观察有了计数数组前后代码的变化
xxxxxxxxxxint cnt1 = 0, cnt2 = 0, cnt3= 0, ......, cnt100 = 0;int cnt[105] = {0};尝试处理预习篇提出的最后1个问题:
xint cnt[105] = {0};for (int i = 0; i < 100; i++) { int t; scanf("%d", &t); cnt[t]++; }// 下面输出每个数字出现的次数
for (int i = 1; i <= 100; i++) { printf("数字%d出现的次数是%d\n", i, cnt[i]);}二、计数数组的基本操作
2.1 一个萝卜一个坑 [模板题]
地上有 10 个坑,分别编号为 0~9,现在,小图灵有 5 粒萝卜种子,他从这 10 个坑中选出了其中的 5个(可重复选择)种上了萝卜种子,请你编写程序,帮小图灵找出哪些坑不会长出萝卜?

输入描述
输入 5 个数,表示小图灵会在这 5 个坑里种上萝卜种子。
输出描述
输出那些没有种萝卜的坑的编号。按从小到大输出。
输入样例
2 4 8 9 2
输出样例
0 1 3 5 6 7
快来试试补完程序
xxxxxxxxxx//尝试填空using namespace std;
int main() { int cnt[?] = {?}; for (int i = 0; i < ?; i++) { int t; scanf("%d", &t); cnt[?]++; } for (int i = ?; i <= ?; i++) { if (?) { printf("%d ", ?); } } }
2.2⭐3步秒懂计数数组
👣Step One
初始化计数数组,这一步的关键是计数数组的长度,想一想如果需要统计的是10000个数字,每个数字出现的次数,数字取值的范围是0到100。
是选
A int cnt[10005] = {0};
还是
B int cnt[105] = {0};
答案是B.
这一步执行后,计数数组cnt会变成这样:
👣Step Two
xxxxxxxxxxfor (int i = 0; i < n; i++) { int t; scanf("%d", &t); cnt[t]++;}在循环中进行统计,统计每个数字出现的频率,一定要理解循环中cnt[t] 表示的是什么。
这步之后计数数组会变成:

👣Step Three
根据题目要求,对计数数组的值进行相应的操作。比如最简单的打印,要求出现过的数字:
xxxxxxxxxxfor (int i = 0; i <= maxn; i++) { if (cnt[i]) printf("%d ", i);}
第三步实际上就是进行扫描。
2.3 用计数数组做排序
排序是将一组“无序”的数据元素调整为“有序”的计算机内操作过程。
生活中排序十分常见,学校的课间操时间,每个班级的同学都会按照高矮个在操场列队。期末考试成绩出来了,老师会按照比分排序,以表扬那些学的好,督促那些还需要进一步努力的同学。
2.3.1身高游戏

先试着写入你家人的身高,比如爸爸、妈妈、爷爷、奶奶和你的身高。
写完后从一边往另一边念,哇,神奇的事情发生了,念出来的数字有序了!刚刚我们做到的就是使用计数数组进行排序。
2.3.2 例题
小图灵大学正在选举新一届学生会,共有 n 名候选人,编号从 1 到 n,最终收集到 m 张选票,每张选票上都写着一个合法的编号。现在请你将所有选票按照候选人编号从小到大进行排序。

输入描述
第一行两个整数 n和 m,第二行 m 个整数。
输出描述
一行,m个整数,为排序后选票上的数字。
输入样例
5
13 17 14 16 12
输出样例
12 13 14 16 17
补充填写这份代码中的???部分:
xxxxxxxxxxusing namespace std;
int main() { int n, m, cnt[???] = {0}; cin >> n >> m; for (int i = 0; i < ???; i++) { int t; cin >> t; cnt[???]++; } for (int i = 1; i <= n; i++) { while (cnt[i]) { printf("%d ", i); cnt[???]--; } } return 0;}####
2.4 课后作业
2.4.1 下面的说法对吗?
1.给定100000个数值范围在0到20000之间的数字,帮助统计每个数字出现次数,计数数组的长度需要开到100005。
2.计数数组不能统计负数和小数出现的频率。
| 2.4.2 编写程序题目 | |
|---|---|
| 阅读题目写输出 | |
| 找字符串中最后一个只出现一次的字符 |
我都完成啦~计数小天才就是我啊!
2.5 更多的练习
| 题目 | 提交情况 |
|---|---|
| 人口增长问题 | NA |
| 矩阵叫换行 | NA |
| 计算矩阵元素边缘之和 | NA |
2.6 真题重现
2.6.1 明明的随机数 [2006普及组]
题目描述
明明想在学校中请一些同学一起做一项问卷调查,为了实验的客观性,他先用计算机生成了 N 个 1 到 1000 之间的随机整数 N <= 100,对于其中重复的数字,只保留一个,把其余相同的数去掉,不同的数对应着不同的学生的学号。然后再把这些数从小到大排序,按照排好的顺序去找同学做调查。请你协助明明完成“去重”与“排序”的工作。
输入格式
输入有两行,第 1 行为 1 个正整数,表示所生成的随机数的个数 N。
第 2 行有 N 个用空格隔开的正整数,为所产生的随机数。
输出格式
输出也是两行,第 1 行为 1 个正整数 M,表示不相同的随机数的个数。
第 2 行为 M 个用空格隔开的正整数,为从小到大排好序的不相同的随机数。
样例输入
xxxxxxxxxx1020 40 32 67 40 20 89 300 400 15
样例输出
xxxxxxxxxx815 20 32 40 67 89 300 400
快去挑战一下!明明的随机数
挑战篇
一、计数排序的复杂度分析
计数排序不是基于比较的排序算法,算法中的循环时间代价都是线性的,还有一个常数k,因此时间复杂度是Θ(n+k)。
二、真题复现 直播获奖 [2020普及组 ]
题目描述
NOI2130 即将举行。为了增加观赏性,CCF 决定逐一评出每个选手的成绩,并直播即时的获奖分数线。本次竞赛的获奖率为 w%,即当前排名前 w% 的选手的最低成绩就是即时的分数线。
更具体地,若当前已评出了 p 个选手的成绩,则当前计划获奖人数为 $\max(1, \lfloor p * w \%\rfloor)$,其中 w 是获奖百分比,$\lfloor x \rfloor$ 表示对 x 向下取整,$\max(x,y)$ 表示 x 和 y 中较大的数。如有选手成绩相同,则所有成绩并列的选手都能获奖,因此实际获奖人数可能比计划中多。
作为评测组的技术人员,请你帮 CCF 写一个直播程序。
输入格式
第一行有两个整数 n, w。分别代表选手总数与获奖率。
第二行有 n 个整数,依次代表逐一评出的选手成绩。
输出格式
只有一行,包含 n 个非负整数,依次代表选手成绩逐一评出后,即时的获奖分数线。相邻两个整数间用一个空格分隔。
样例 #1
样例输入
xxxxxxxxxx10 60200 300 400 500 600 600 0 300 200 100
样例输出
xxxxxxxxxx200 300 400 400 400 500 400 400 300 30
提示
样例 1 解释
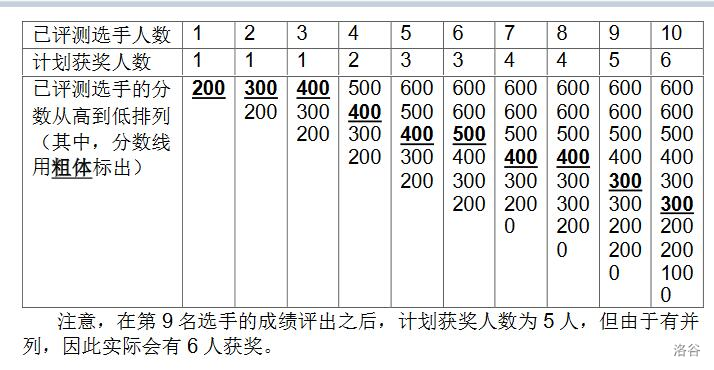
数据规模与约定
各测试点的 n 如下表:
| 测试点编号 | n= |
|---|---|
| 1 ~ 3 | 10 |
| 4 ~ 6 | 500 |
| 7 ~ 10 | 2000 |
| 11 ~ 17 | 10^4 |
| 18~ 20 | 10^5 |
对于所有测试点,每个选手的成绩均为不超过 600 的非负整数,获奖百分比 w 是一个正整数且 1 < w < 99。
提示
在计算计划获奖人数时,如用浮点类型的变量(如 C/C++ 中的 float 、 double)存储获奖比例 w%,则向下取整后的结果不确定。因此,建议仅使用整型变量,以计算出准确值。
快来挑战!直播获奖
三、更多的挑战题目
我完成啦!